I'm Bryan. This is my blog of the following projects (links above):
Hack for Heat
In my free time, I volunteer for Heat Seek, an NYC based non-profit that deploys temperature sensors to ensure that everyone in the city has adequate heating over the winter. My posts aim to show some of the groundwork that goes into writing some of our blog posts.
Mediocre Museum
The mediocre part of this project comes from my friend Emilia's and my goal of building the most average artifact possible. We're currently working with open data obtained from the Canada Science and Technology Museums Corporation, obtainable here.
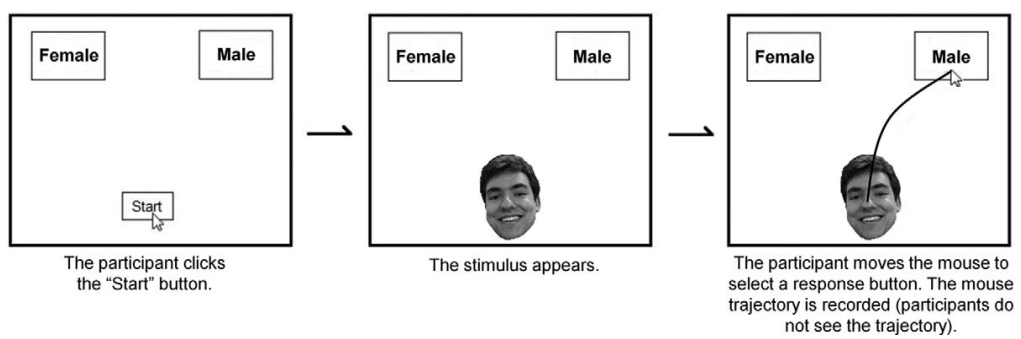
Mousetracker Data
I'm working with my colleagues, Qi Xu and Carlina Conrad, at the NYU Couples Lab to learn more about how people in relationships allocate resources amongsts themselves, and balance self-, altruistic, and group interests.
Skytrax Ratings
What makes a good flight? Using Skytrax ratings data scraped by Quang Nguyen, I'm investigating what factors make up a passenger's overall rating, as well as what influences their decision to recommend an airline to others (vs. not).

 Also, this looks like a regular car:
Also, this looks like a regular car:
 These just look like very understandable typos, but they also suggest that we should use the median, which is relatively unaffected by these issues.
These just look like very understandable typos, but they also suggest that we should use the median, which is relatively unaffected by these issues.